Excel VBAで＜てこ比＞を求める関数を作ってみた

前回は、Excel分析ツールの回帰分析の結果から、Ｒの「基本的診断プロット」と同じグラフを作れんものかとチャレンジしましたが、Residuals vs Leverage まで来たところで、てこ比をどうしようか、となって終わりました。

そこで今回は、Excelでてこ比を計算してみたいと思います。

計算方法ですが、

RとRコマンダーではじめる多変量解析

作者: 荒木孝治
出版社/メーカー: 日科技連出版社
発売日: 2007/10/01
メディア: 単行本
クリック: 3回
この商品を含むブログ (8件) を見る

の73ページに、

射影行列（式(3.57)）の対角要素 $hii$ を、てこ比またはレベレッジ（Leverage）という。

また、70ページに、

$y$ の係数を $H$ とし、その要素を、

$H=X(X^TX)^{-1}X^T=\begin{pmatrix}h_{11}　\ldots　h_{1n} \\ \vdots　 \ddots　\vdots　 \\ h_{n1}　\ldots　h_{nn}\end{pmatrix}$

とおく。 $H$ を射影行列という。（略）ハット行列ともいう。

さらに、54ページに

$X=\begin{pmatrix}1　x_{11}　x_{12}　 \\ 1　x_{21}　x_{22}　 \\ \vdots　　 \vdots　　\vdots　　　 \\1　x_{n1}　x_{n2}　\end{pmatrix}$

とあります。

射影行列（ハット行列）は、最小二乗法で計算するときに導かれる行列らしいのですが、私自身がまだ十分に理解できていないので、ここで解説することはできません。

が、上の手がかりさえあれば、計算そのものは進めることができます。

$X$ は、説明変数が二つの場合を表していて、 $x_{i1},x_{i2}$ がそれにあたります。
ちなみに、左側に並んでいる「1」は切片のための列だそうで、切片は定数項なので「1」となります。*1
あとは、行列の計算で $H$ を求めて、対角要素を抽出するだけです。
（ちなみに、 $X^T$ は $X$ の転置行列、 $X^{-1}$ は $X$ の逆行列を表します。）

まず、説明変数を新しいワークシートのＢ列にコピーします。
そして、Ａ列に（説明変数と同じ行数分）「1」を入力しておきます。

f:id:cyclo-commuter:20190905134418p:plain

入力＆コピペしたセル範囲が $X$ です。

$X$ を選択して、コピー→Ｅ１セルを選択→［貼り付け］→［行列を入れ替える］をクリック。

f:id:cyclo-commuter:20190905135631p:plain

f:id:cyclo-commuter:20190905135910p:plain

これが、 $X^T$ です。

$X^TX$ を計算しましょう。

あらかじめE4:F5のセル範囲を選択しておく→数式バーに行列の積の計算式*2を入力→【Ctrl】＋【Shift】＋【Enter】キーを押下。

f:id:cyclo-commuter:20190905140243p:plain

f:id:cyclo-commuter:20190905140813p:plain

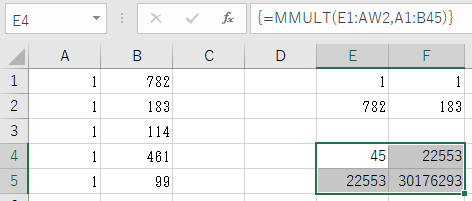
続いて、これの逆行列を計算します。

あらかじめH4:I5のセル範囲を選択しておく→数式バーに逆行列の計算式を入力→【Ctrl】＋【Shift】＋【Enter】キーを押下。

f:id:cyclo-commuter:20190905140949p:plain

f:id:cyclo-commuter:20190905141556p:plain

$(X^TX)^{-1}$ が求まりました。

次は、 $X(X^TX)^{-1}$ です。

あらかじめE7:F51のセル範囲を選択しておく→数式バーに行列の積の計算式を入力→【Ctrl】＋【Shift】＋【Enter】キーを押下。

f:id:cyclo-commuter:20190905142133p:plain

f:id:cyclo-commuter:20190905142241p:plain

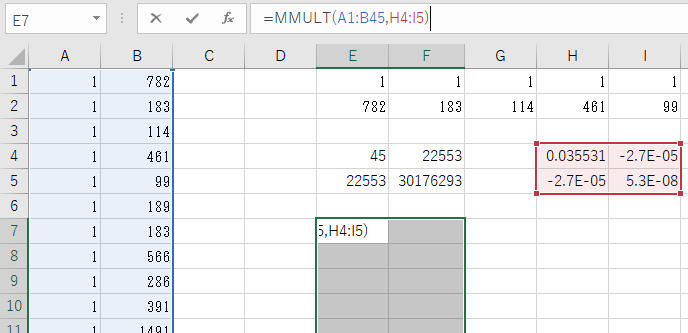
最後は、 $H=X(X^TX)^{-1}X^T$ 。

あらかじめH7:AZ51のセル範囲を選択しておく→数式バーに行列の積の計算式を入力→【Ctrl】＋【Shift】＋【Enter】キーを押下。

f:id:cyclo-commuter:20190905142601p:plain

f:id:cyclo-commuter:20190905142713p:plain

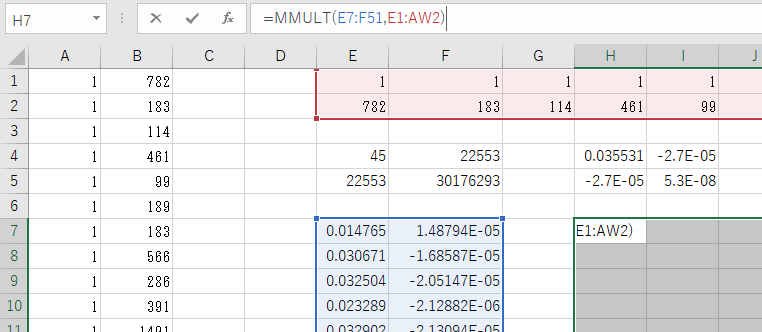
はい！　射影行列（ハット行列）の出来上がり！

では、対角要素を抽出しましょう。

C1セルに「=OFFSET($G$6,ROW(),ROW())」と入力して、C45セルまでコピーします。

f:id:cyclo-commuter:20190905143237p:plain

f:id:cyclo-commuter:20190905143533p:plain

以上、てこ比が計算できました！！　けっこうな手間ですねえ。

しかし、このめんどくさ～い計算をExcel VBAで記述すると、

'てこ比を返す
Function Leverage(RNG As Range)

    Dim buf, tmp(), i

    With Application.WorksheetFunction
        buf = .MMult(.MMult(RNG, .MInverse(.MMult(.Transpose(RNG), RNG))), .Transpose(RNG))
    End With
        
    ReDim tmp(UBound(buf) - 1, 0)
    For i = LBound(buf) To UBound(buf)
        tmp(i - 1, 0) = buf(i, i)
    Next
    Leverage = tmp

End Function

これだけで済んじゃうんです。

使い方はいつものとおり、ソースコードを標準モジュールにコピペしたら、普通の関数のようにセルに入力するだけ。

あらかじめC1:C45のセル範囲を選択しておく→数式バーに「=Leverage(A1:B45)」と入力→【Ctrl】＋【Shift】＋【Enter】キーを押下。

f:id:cyclo-commuter:20190905150842p:plain

f:id:cyclo-commuter:20190905151003p:plain

ほら、楽々計算できましたよ ♪

それでは、前回積み残しになっていたResiduals vs Leverage のグラフを作ってみましょうか。

横軸にてこ比、縦軸に標準化残差を取って散布図を作ると、

f:id:cyclo-commuter:20190905153437p:plain

こんな感じです。

なんというか、分布は他の診断図と同様に東京の座標を除いてＲの出力結果と同じですが、クックの距離を表す補助線がないと、診断のしようがないですねえ。

f:id:cyclo-commuter:20190905153734p:plain

うーん、残念無念。

あ、そうそう、東京の座標がExcelとRで異なる件ですが、『RとRコマンダーではじめる多変量解析』の70ページにこうありました。

残差 $e_{i}$ を標準化して、それを利用して誤差の家庭のチェックに利用する。標準化の方法はさまざま提案されている。 $h_{ii}$ をハット行列の対角要素とするとき、
$\acute{e_{i}}=\frac{e_{i}}{\sqrt{(1-h_{ii})V_{e}}}$
を標準化残差（standardized residual）という。

（下線引用者）