標本平均の分布が正規分布になることをシミュレーションで確かめてみた２

前回は、の母集団からの標本を1000回抽出し、標本分布を作るところまで行いました。

今回は、サンプルサイズの大きさや母集団の分布の形によって、標本分布の形・標本平均の平均・標本平均の分散がどう変わるかを確認してみたいと思います。

1. 前回の最後に作成したヒストグラムに、の正規分布曲線を重ねてみます。

   

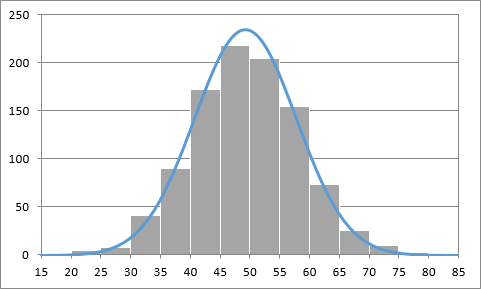
   n=10の標本分布とN(49,73.6)の正規分布

   うん、大体重なってますね。理論どおりと言ってよいでしょう。

2. 次に、サンプルサイズをにして、同じようにグラフにしてみます。

   

   n=5の標本分布とN(49,147.2)の正規分布

   標本分布が正規分布に対して少し歪んでいますね。でも、これくらいならまだ「正規分布に従っている」と言ってもよさそうです。

3. では、サンプルサイズをもっと小さく、にしてみましょう。

   

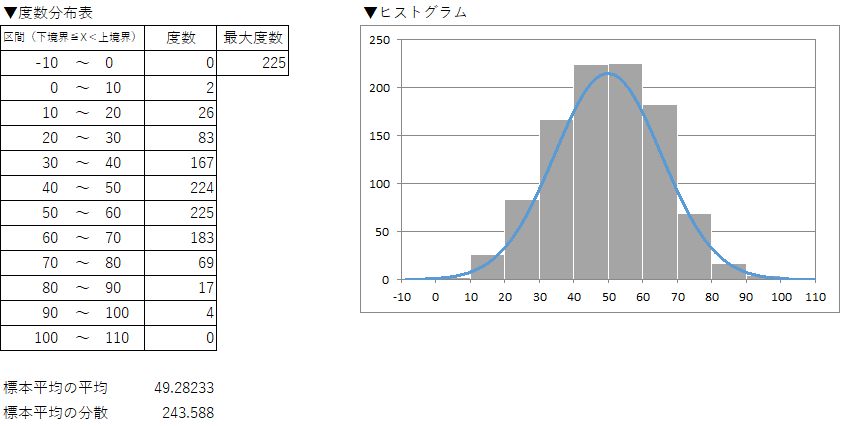
   n=3の標本分布N(49,245.3)の正規分布

   分散が大きくなったぶん階級幅も広がったため、もさっとした印象ですが、思ったよりも正規分布に近い形を保っているように見えます。

4. では、母集団の分布を変えてみましょう。

   

   N=1000, べき分布の母集団

   今度は、母集団をべき分布にしてみました。

   

   n=10の標本分布とN(20,63.3)の正規分布

   

   n=5の標本分布とN(20,126.6)の正規分布

   

   n=3の標本分布とN(20,211)の正規分布

   で既に歪みが感じられますが、になると完全に正規分布からずれてしまってますね。

5. 今回のシミュレーションでは、サンプルサイズでも、分布は正規性を保っているように見えましたが、 一般的には、母集団の分布が未知または正規分布に従わない場合、標本平均の分布が正規分布に（近似的に）従うと言えるのは、サンプルサイズがのときだそうです。

今回のシミュレーションでは、標本平均の分布は正規性について意外と頑健という結果になりましたが、小さいサンプルサイズでは信頼区間の幅がやたらと大きくなって（バラツキが大きくなって）*1、分析結果が実用に耐えないと思われますので、その点はご留意ください。

*1:母平均の95％信頼区間はですから、4.の例について、サンプルサイズ10のときの母平均の95％信頼区間は、標本平均の平均を使ったとしても、
これを解いて、4.69以上35.89以下となります。