Excel VBAでクロス表からクラメールのＶを求める関数を作ってみた

今回は、カイ二乗検定とセットで説明されることが多いクラメールのＶに挑戦してみます。

クラメールのＶは連関係数とも独立係数とも呼ばれ、縦・横の２変数間の関連の度合いを表すことができるようです。0≦Ｖ≦１で、１に近づくほど関連が大きい由。

手順としては、

1. カイ二乗検定　→　帰無仮説「２変数は独立」が棄却されたら、
2. クラメールのＶで関連の度合いを確認

といった感じでしょうか。
このクラメールのＶ、なんと前回「使いみちが分からん」と言ったカイ二乗値を元に計算されます。泥縄ぶりが露呈してますね。

さて、こんな表を用意してみました。（データは架空のものです。）

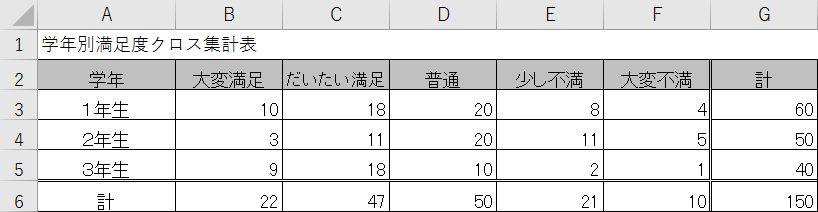
前回、前々回に作った関数でカイ二乗検定をしてみると、

有意水準0.05で帰無仮説「学年と満足度は独立」が棄却されました。
では、さっそく自作した関数でクラメールのＶを計算してみましょう。
ソースコードは以下のとおりです。*1

'クロス表からクラメールのＶを求める
Function Cramer_V(Arg)

    Dim o_Row As Integer
    Dim o_Clm As Integer
    Dim o_R_Sum() As Long
    Dim o_C_Sum() As Long
    Dim o_Sum As Long
    Dim i As Integer
    Dim j As Integer
    Dim o As Double
    Dim e As Double
    Dim o_e2 As Double
    Dim RC As Integer

    o_Row = Arg.Rows.Count
    o_Clm = Arg.Columns.Count
    ReDim o_R_Sum(1 To o_Row)
    ReDim o_C_Sum(1 To o_Clm)

    For i = 1 To o_Row
        For j = 1 To o_Clm
            o_R_Sum(i) = o_R_Sum(i) + Arg(1).Offset(i - 1, j - 1)
            o_C_Sum(j) = o_C_Sum(j) + Arg(1).Offset(i - 1, j - 1)
            o_Sum = o_Sum + Arg(1).Offset(i - 1, j - 1)
        Next
    Next
    For i = 1 To o_Row
        For j = 1 To o_Clm
            o = Arg(1).Offset(i - 1, j - 1)
            e = o_C_Sum(j) * o_R_Sum(i) / o_Sum
            o_e2 = o_e2 + ( (o - e) ^ 2) / e
        Next

    Next
    RC = WorksheetFunction.Min(Arg.Rows.Count, Arg.Columns.Count) - 1

    Cramer_V = Sqr(o_e2 / (o_Sum * RC))
    
End Function

引数は、例によって［実測値範囲］のみです。
結果は、0.2323...となりました。「弱い関連がある」と言ったところでしょうか。
このクラメールのＶ、ピアソンの積率相関係数と比べるとかなりマイナーで、ネットで調べても目安が今ひとつはっきりしません。某所で「V=0.17はかなり大きい」旨の説明を受けたこともあるのですが、果たして本当に？

*1:2017/12/23 コード個所をpre記法に直しました